Learning from Failure to Tackle Extremely Hard Problems

This is a blog post about our work on BaNEL: Exploration Posteriors for Generative Modeling Using Only Negative Rewards (https://arxiv.org/abs/2510.09596).

Tackling Very Hard Problems

The ultimate aim of machine learning research is to push machines beyond human limits – to solve problems that humans cannot. But can today’s AI actually do that?

GPT-5 receives a zero reward.

For example, I once asked GPT-5 to design a cure for cancer. It failed. If I try again, will it succeed? Probably not. How many attempts would it take? We expect the success probability to be nonzero (since GPT-5, being an autoregressive generative model, never assigns exactly zero probability to any finite sequence), but at best, it’s vanishingly small. Worse still, evaluating the solution is expensive and risky, since it requires actual clinical trials.

This illustrates a broader issue: the hardest and most important problems are those with near-zero success rates – and no positive examples available during learning. Under such extreme reward sparsity, standard post-training methods like policy gradients (including GRPO) collapse into brute-force random search, since zero rewards produce zero gradients. If we cannot address this, post-training will be limited to distribution sharpening rather than unlocking genuinely new capabilities beyond training data.

Learning from Negative Rewards

To tackle this, we need algorithms that can learn from failures alone—using only negative reward samples—while minimizing the number of reward evaluations (NREs). Why do we think that this would be even possible? There’s a simple (if impractical) way to see that it’s at least theoretically doable.

Do not make the same mistake twice! If our budget for evaluating $r$ were unlimited, and assuming the solution has bounded length, we could trivially achieve a perfect success rate by collecting every possible mistake $R:=\{\mathbf{x} \mid r(\mathbf{x})=0\}$ and avoiding all elements of $R$ :

\[p_{\boldsymbol{\theta} \mid R^C}(\mathbf{x}) \propto p_{\boldsymbol{\theta}}(\mathbf{x}) \mathbf{1}[\mathbf{x} \notin R],\]

where $p_{\boldsymbol{\theta}}$ is the pre-trained generative model (e.g., GPT-5). $p_{\boldsymbol{\theta} \mid R^C}(\mathbf{x})$ means we condition the model on the complement of $R$ by multiplying the indicator function. This formulation says: once you’ve seen all possible failures, you’ll never make a new one.

Exploiting the structure underlying failures. Of course, this approach is infeasible because the space of failures is combinatorial, and we want to minimize NREs. But crucially, in most intelligent tasks we care about, failures are not arbitrary: they have patterns that distinguish them from successes (otherwise, intelligence does not matter). If we can learn these patterns, we can approximate $R$ using a small number of samples. This parallels how human scientists reason: they generalize from failures, avoiding past mistakes without discarding promising directions. To minimize NREs, the algorithm must extract as much information as possible from failures before making new attempts.

Minimizing NREs requires heavy computation to fully exploit past failures before costly new attempts (e.g., clinical trials).

Learning a Generative Model of Failures

Our idea is to model regularities underlying failures using a separate generative model $p_\phi$ trained only on failed attempts. Generative modeling is a powerful unsupervised way for learning structure from data – and scales extremely well!

Specifically, we train a separate generative model $p_\phi$ (parameterized by $\phi$ ) on $m$ negative examples with the standard maximum likelihood objective:

\[\max _{\boldsymbol{\phi}} \frac{1}{m} \sum_{i=1}^m \log p_{\boldsymbol{\phi}}(\mathbf{x}_i) .\]

Once well-trained, $p_\phi(\mathbf{x})$ can be used to assess whether a given input resembles previously observed failures; specifically, we use $p_\phi$ to define a rejection region $\tilde{R}$ approximating $R$:

\[\tilde{R}:=\lbrace \mathbf{x}: \frac{p_{\boldsymbol{\theta}}(\mathbf{x})}{p_{\boldsymbol{\phi}}(\mathbf{x})}<\tau \rbrace\]

where $\tau$ is a threshold value. Note that this requires $p_{\boldsymbol{\theta}}$ and $p_\phi$ to be likelihood-based generative models under which we can compute the likelihood (e.g., autoregressive models). Using the rejection region $\tilde{R}$, we form a Bayesian posterior $\tilde{p}_{\boldsymbol{\theta}}$ to approximate $p_{\boldsymbol{\theta} \mid R^C}$ :

\[p_{\boldsymbol{\theta} \mid \tilde{R}^C}(\mathbf{x}) \propto p_{\boldsymbol{\theta}}(\mathbf{x}) \mathbf{1}[\mathbf{x} \notin \tilde{R}],\]

This posterior filters out data points that are similar to prior failures according to $\tilde{R}$; equivalently, we direct the model to sample only from $\tilde{R}^C$.

Online Recursive Update

Once we improve the generative model using the Bayesian update as described above, we can use it to gather another batch of $m$ samples. Here, rejection regions from earlier rounds can be accumulated by taking their union (i.e., $\tilde R \gets \tilde R \cup \tilde R_{\text{new}}$ where $R_{\text{new}}$ is the new rejection region). This can be repeated multiple times, as illustrated in the figure below. We call this method BaNEL: Bayesian Negative Evidence Learning.

Illustration of BaNEL on a 1D toy example. The procedure begins with a pre-trained proposal distribution (leftmost). Two reward-one samples (red bars) are located at -2 and 2. At each iteration, the proposal distribution generates samples, which are very likely to be 0-reward. These are used to train a negative model (red dashed curves). The proposal and negative models are combined to form the Bayesian posterior (black curves). As iterations progress, the posterior increasingly concentrates on the reward-one regions, until convergence (rightmost).

Experiment: Adversarial Attack On Toy Language Model

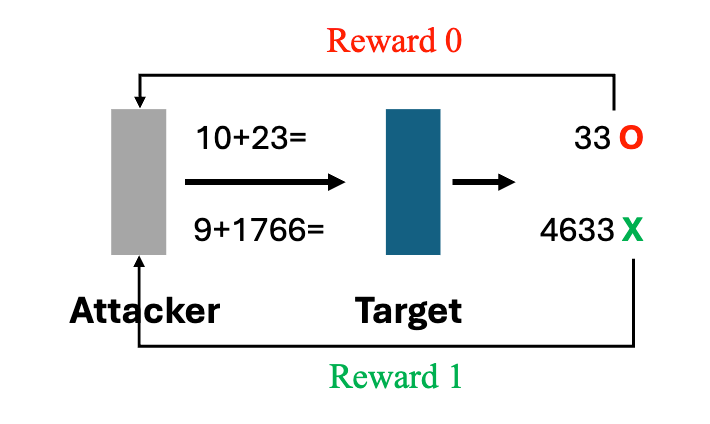
In this task, the goal is to attack the target model, an autoregressive transformer trained to answer digit-addition queries (e.g., it receives 10+23= and must generate 33). The goal of the attacker model, also an autoregressive transformer pre-trained on the same dataset to generate questions such as 10+23=, is to propose syntactically valid addition queries on which the target model produces an incorrect sum. That is, the reward is defined as:

• $r(\mathbf{x}) = 1$ if $\mathbf{x}$ is a syntactically valid arithmetic expression and the target’s output is incorrect,
• $r(\mathbf{x}) = 0$ otherwise.

Since the target is trained well, the pre-trained attacker’s empirical success rate is roughly 0.0004. We set a hard limit on NREs: $r$ can only be evaluated 7500 times at most. All reward-1 samples are filtered out during training – forcing the model to learn only from failures.

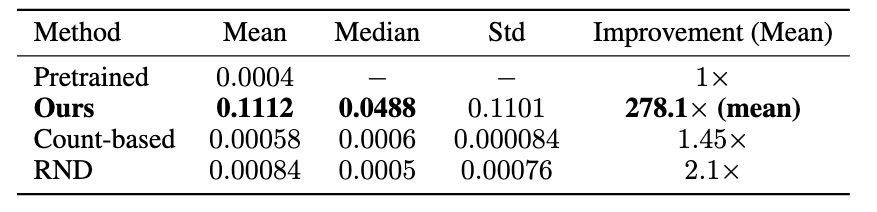As shown in this table, BaNEL improves the success rate by 278x on average, outperforming baselines by several orders of magnitude.

Successful attacks generated by BaNEL.

BaNEL identifies two failure modes of the target:

1. Leading zeros: when at least one of the input digits starts with at least one zero, the output result tends to be incorrect. This is likely because the training data (shared by both the target and the attacker) does not contain any examples with leading zeros.
2. Carry-chain stressors: examples that need to carry a digit during summation.

Based on these identified patterns, we designed a rule-based attack and observed that it achieves near-perfect success rate. This suggests that BaNEL can be used not only to increase a numeric success rate, but also to guide human intuition on hard problems to extract qualitative insights.

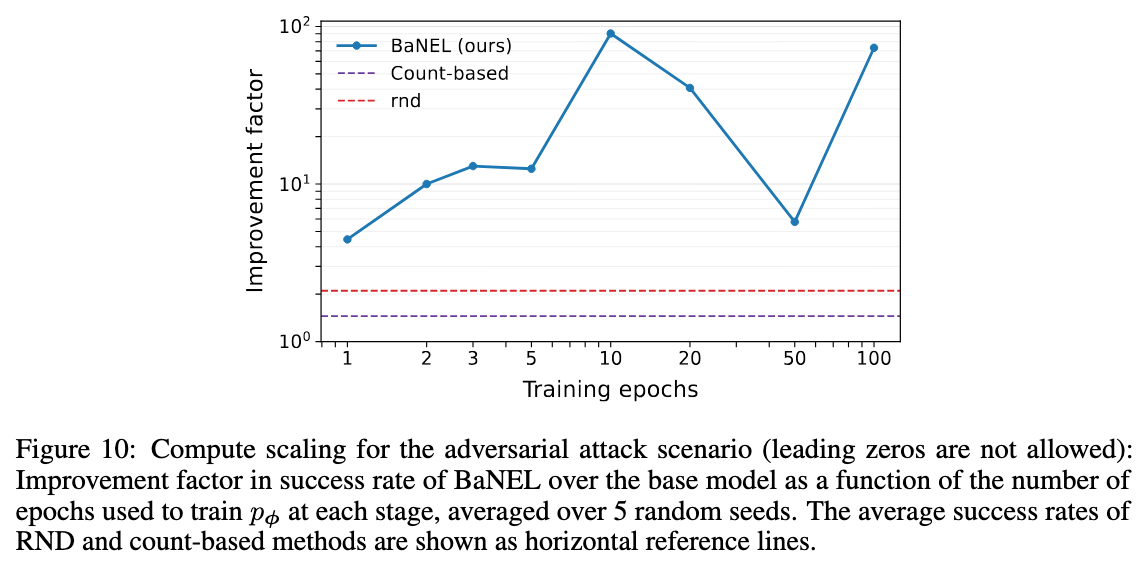
We also study scaling with compute (here we don’t allow leading zero attacks to make the problem even more challenging). When the negative generative model $p_\phi$ is under-trained (few epochs), BaNEL performs on-par with simpler novelty-bonus baselines (RND, pseudo-counts). But as we spend more compute on $p_\phi$ (without additional NREs), BaNEL outperforms these methods by a large margin. This highlights a key property: BaNEL trades compute for reward efficiency. It is suboptimal under strict compute limits but excels when additional offline computation is available.

Experiment: Language Model Reasoning

We further evaluate BaNEL on reasoning tasks using GSM8K subsets, where the pre-trained Qwen 2.5 0.5B model (further fine-tuned on GSM8K using PPO) performs poorly. Again, all reward-1 samples are filtered out during training.

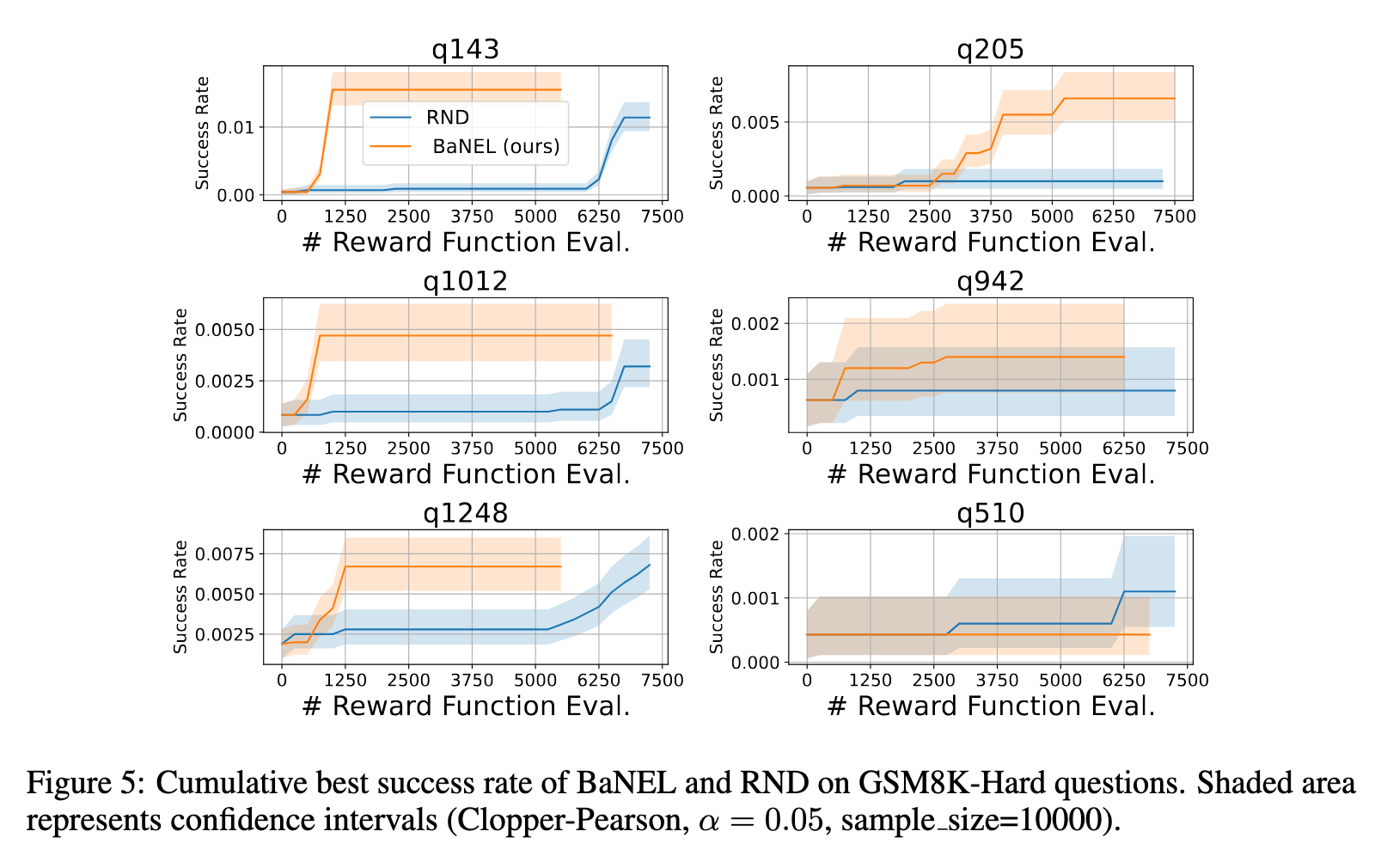
For most problems, BaNEL substantially improves success rates over the pre-trained baseline, outperforming RND with fewer reward evaluations.

Closing Remarks

By modeling failures with a generative model, BaNEL turns negative evidence into a learning signal, enabling exploration in settings where reward = 1 samples are nearly nonexistent. While BaNEL is only a first step towards learning in this challenging regime, we view it as an important direction for the generative modeling field: to truly push the frontier of what generative models are capable of, we must learn to learn from failures!

Check out our paper for more results and details!

Paper link: https://arxiv.org/abs/2510.09596